>Rpncalc
Last Edit: May 4, 2019, 1:47 a.m.
But I wasn't happy with what I found. I definitely wanted it to use RPN, be able to handle functions, and show the current stack. I also wanted variables, to be able to load programs from files, and to run in the terminal.
This website lists a bunch of RPN calculators. A few of them are real close to doing what I wanted, but none of them were quite right. So I decided to roll my own.
Here are the built in operations.
Math
All math operations pop the last two items from the stack, then push the result. The math works as expected when one of the operands is a float, you get a float result
Initial stack:
| Position | Initial | + | - | * | / | % | ^ | |
|---|---|---|---|---|---|---|---|---|
| infix equivalent | #1 + #0 | #1 - #0 | #1 * #0 | #1 / #0 | #1 % #0 | #1 ^ #0 | ||
| #4 | 1 | |||||||
| #3 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | |
| #2 | 3 | 2 | 2 | 2 | 2 | 2 | 2 | |
| #1 | 4 | 3 | 3 | 3 | 3 | 3 | 3 | |
| #0 | 5 | 9 | -1 | 20 | 0 | 1 | 1024 |
Stack Control
Stack control operations move items around on the stack. dup, over, tuck, and pick add an item to the stack. Drop removes one. The backtick ` can be used as a shorthand for drop.
| Position | Initial | swap | dup | rot | over | tuck | 3 pick | 3 roll | drop | |
|---|---|---|---|---|---|---|---|---|---|---|
| #4 | 1 | 1 | 1 | 1 | ||||||
| #3 | 1 | 1 | 2 | 1 | 2 | 2 | 2 | 2 | ||
| #2 | 2 | 2 | 3 | 3 | 3 | 4 | 3 | 3 | 1 | |
| #1 | 3 | 4 | 4 | 4 | 4 | 3 | 4 | 4 | 2 | |
| #0 | 4 | 3 | 4 | 2 | 3 | 4 | 1 | 1 | 3 |
Comparisons
The comparisons would take the infix form of #0 <operator> #1, and return 1 if true and 0 if false.
| Position | Initial | == | > | < | >= | <= | |
|---|---|---|---|---|---|---|---|
| #4 | |||||||
| #3 | 1 | ||||||
| #2 | 2 | 1 | 1 | 1 | 1 | 1 | |
| #1 | 3 | 2 | 2 | 2 | 2 | 2 | |
| #0 | 3 | 1 | 0 | 0 | 1 | 1 |
| Position | Initial | == | > | < | >= | <= | |
|---|---|---|---|---|---|---|---|
| #4 | |||||||
| #3 | 1 | ||||||
| #2 | 2 | 1 | 1 | 1 | 1 | 1 | |
| #1 | 3 | 2 | 2 | 2 | 2 | 2 | |
| #0 | 4 | 0 | 1 | 0 | 1 | 0 |
| Position | Initial | == | > | < | >= | <= | |
|---|---|---|---|---|---|---|---|
| #4 | |||||||
| #3 | 1 | ||||||
| #2 | 2 | 1 | 1 | 1 | 1 | 1 | |
| #1 | 3 | 2 | 2 | 2 | 2 | 2 | |
| #0 | 2 | 0 | 0 | 1 | 0 | 1 |
Conditionals
The two conditionals work similarly, but pop a different number of parameters.
They resolve to true if and only if the ? value is 1 or 1.0. IfTrue or IfFalse can be any data type. If they are substacks, they will be immediately executed. To anonymously return a substacks, a simple nested substack will suffice. (ex: [ 4 ] will return 4 from the if block, but [ [ 4 ] ] will return the substack [ 4 ].
| Position | Initial | if | |
|---|---|---|---|
| #4 | N/A | N/A | |
| #3 | N/A | N/A | |
| #2 | N/A | N/A | |
| #1 | ? | N/A | |
| #0 | IfTrue | IfTrue |
| Position | Initial | ifelse | |
|---|---|---|---|
| #4 | N/A | N/A | |
| #3 | N/A | N/A | |
| #2 | ? | N/A | |
| #1 | IfTrue | N/A | |
| #0 | IfFalse | Result |
Substacks
"Substacks" can be though of as functions, lists, routines, and objects. To execute a substack, use the ! operator. To "instantiate" a substack, use the !! operator This effectively executes the substack just like ! but instead of pushing new values onto the main stack, it creates a new substack holding them. If for some reason an error occurs during function execution, the stack is reverted to its state before execution started.
| Position | Initial | ! | |
|---|---|---|---|
| #4 | |||
| #3 | 3 | 3 | |
| #2 | 2 | 2 | |
| #1 | 1 | 1 | |
| #0 | [ 3 ] | 3 |
| Position | Initial | !! | |
|---|---|---|---|
| #4 | |||
| #3 | 3 | 3 | |
| #2 | 2 | 2 | |
| #1 | 1 | 1 | |
| #0 | [ 3 ] | [ 3 ] |
You can create substacks on the fly by using the group operator. It pops the last item on the stack and groups that many items into a substack. You can also grow a substack using the append and prepend operators. The cat operator combines two substacks together into one if needed.
| Position | Initial | group | append | prepend | 7 8 cat | cat | |
|---|---|---|---|---|---|---|---|
| #5 | 6 | ||||||
| #4 | 5 | ||||||
| #3 | 4 | ||||||
| #2 | 2 | 6 | |||||
| #1 | 1 | 5 | 6 | [ 6 5 2 1 5 ] | |||
| #0 | 3 | [ 4 2 1] | [ 4 2 1 5 ] | [ 6 5 2 1 5 ] | [ 7 8 ] | [ 6 5 2 1 5 7 8 ] |
Note that group and cat look similar, but group preserves and embeds lists while cat joins them.
You can access items in a substack using the \ operator. You can similarly get the size of a substack using \size .
You can use \ to get items from an array.
The accessed item can be a variable on the stack.
| Position | Initial | 0 \ | drop 1 \ | drop 2 \ | drop 4 \ | |
|---|---|---|---|---|---|---|
| #5 | ||||||
| #4 | ||||||
| #3 | ||||||
| #2 | ||||||
| #1 | [ 1 2 3] | [ 1 2 3] | [ 1 2 3] | [ 1 2 3] | ||
| #0 | [ 1 2 3] | 1 | 2 | 3 | NULL |
Or part of the instruction
| Position | Initial | \2 | |
|---|---|---|---|
| #5 | |||
| #4 | |||
| #3 | |||
| #2 | |||
| #1 | [ 1 2 3] | ||
| #0 | [ 1 2 3] | 3 |
Or it can be used with the SIZE instruction
| Position | Initial | \size | |
|---|---|---|---|
| #5 | |||
| #4 | |||
| #3 | |||
| #2 | |||
| #1 | [ 1 2 3 2 1] | ||
| #0 | [ 1 2 3 2 1 ] | 5 |
You can also use \varname to read a variable name out of a substack that has been instatiated with !!.
| Position | Initial | !! \a | |
|---|---|---|---|
| #5 | |||
| #4 | |||
| #3 | |||
| #2 | |||
| #1 | [ 1 2 3 a =] | ||
| #0 | [ 1 2 3 a = ] | 3 a = |
When executed, substacks run in a sub-interpreter where they have access to any variables previously defined and can pop items from their parent interpreters stack. If a variable does not exist in their parent (or their parent's parent recursively) then a temporary variable is created that gets unbound to a constant when the execution exits. Whatever is in the stack at the end of the substack's execution gets pushed onto the end of its parents stack (or a sub-stack with !! ), with all variables not in the parent scope resolved to their values and functions made anonymous. Variables can be declared as local only by prefixing the variable name with a $. Variables defined in this way will not show up in the parent or any child interpreters.
Anything that can go out of a substack can go inside of one, including substacks. Since the parent interpreters variables are available, recursion is possible. For example, here is a program that calculates the factorial of the last number on the stack.
The provided interface can automatically load commands at startup. It will read in all the files from the *auto_functions_directory* which is defined in the settings file. All files in this directory with extension ".rpn" are read in and interpreted line by line. Because they are dumped directly into the interpreter, it is recommended that everything in the files be assigned to a variable and then dropped off the stack so you start with a blank stack, but new pre-defined variables. A few of these are included for convenience such as all which returns 1 if there are items on the stack and 0 if there are not and fact which returns the factorial of the last number on the stack. This is also where you will find foreach and reverse which operate on lists as you might expect.
[ dup # copy the item we are factorializing 1 - # decrement it 0 < # until it reaches zero [ # if greater than 0 dup # set up the value we are passing to the next recursion 1 - # it is one less than the starting value fact ! # recurse * # multiply the result of recursion by the original value ] if ] fact = # set up the function name so we can recurse to it drop
Looping
There is a single looping construct, while.
While takes a function as its argument and executes it. It then pops the last item from the stack and uses that value to determine if the function should be executed again, or if execution should end. A 1 will continue execution, anything else will end it. At any time during the loop, break can be used to end the loop early. For example, [ + size 1 < ] while can be used to add all items in the stack. [ 5 == [ break ] if 1 ] while can be used to purge items on the stack until you reach a 5 (of course, you could use [ 5 == not ] while to achieve the same thing. )
Variables
To define a variable, you just enter whatever string you want as long as it does not contain any of the built in operator names or characters. If the variable is unassigned, this will create a new variable with a value of 0. If it has already been assigned, it will push the variable onto the stack.
Assuming the variable abc has a value of 5 from a previous assignment:
| Position | Initial | var | abc | |
|---|---|---|---|---|
| #4 | 3 | |||
| #3 | 3 | 2 | ||
| #2 | 3 | 2 | 1 | |
| #1 | 2 | 1 | var=0 | |
| #0 | 1 | var=0 | abc=5 |
Assignment is handled with the = operator. The value in position #0 must be a variable. The value of position #1 is assigned to the variable. If position #1 is a function, the variable name becomes the function name.
| Position | Initial | = | |
|---|---|---|---|
| #4 | |||
| #3 | 3 | ||
| #2 | 2 | 3 | |
| #1 | 1 | 2 | |
| #0 | var=0 | var=1 |
If a variable name starts with a $, it is local (and local only - called functions will no be able to access it either)
Other
Comments can be added to anything on the stack using the apostrophe ' . Simply enter any valid variable name and then use the comment operator. The variable is unbound and the variable name is used for the comment. You can see this in the video below. When both arguments to basic math operations have comments, the comments are combined and retained.
Code comments are indicated by a hash #. Anything after the # is ignored on each parsed line.
The int command converts a variable or float to an integer. The float command converts a variable or integer to a float. These commands are useful to push the value of a non-local variable value onto the stack from a function.
Operator plugins written in python are supported in the supplied interface. All .py files in the plugins directory are imported and their register() function is called. This function needs to return a dictionary where keys = the operator string you want to use and the value = the function it should call. All functions have to take the current interpreter as their first parameter. Any additional parameters will be popped off the stack and passed in. Note that this means the values are passed in reverse order (last item on the stack is parameter 1, etc). The values will be whatever type they are stored on the stack as (either a Value, Variable, or Function), so if you want to use the actual value, make sure to use the val property. All the default operators defined in the rpncalc.py file are defined in the same way the plugin operators need to be so you can look at that for inspiration.
Here is an example of a plugin that maps the python math module to usable operators in the interpreter in the form of math.operator
#####################################################################################
#
# the builtin functions in math are C functions, so I can't introspect into their
# function parameters. So, I'll just hard code the quantity. The dicts were
# created by copying the result of dir(math) out of a shell and trimming them.
import rpncalc
import math
def noparam_gen(constant):
return lambda interp: [rpncalc.Value(math.__dict__[constant])]
noparam = ['e', 'pi']
def oneparam_gen(function):
return lambda interp, a : [rpncalc.Value(math.__dict__[function](a.val))]
oneparam = ['acos',
'acosh',
'asin',
'asinh',
'atan',
'atanh',
'ceil',
'cos',
'cosh',
'degrees',
'erf',
'erfc',
'expm1',
'fabs',
'factorial',
'floor',
'frexp',
'gamma',
'isinf',
'isnan',
'lgamma',
'log10',
'log1p',
'modf',
'exp',
'radians',
'sin',
'sinh',
'sqrt',
'tan',
'tanh',
'trunc']
def twoparam_gen(function):
return lambda interp, a, b : [rpncalc.Value(math.__dict__[function](a.val, b.val))]
twoparam = ['copysign',
'fmod',
'ldexp',
'log',
'atan2',
'hypot']
def register():
result = {}
for const in noparam:
result['math.%s' % const] = noparam_gen(const)
for func in oneparam:
result['math.%s' % func] = oneparam_gen(func)
for func in twoparam:
result['math.%s' % func] = twoparam_gen(func)
return result
Interface
The interface supports commands which do things outside of the main interpreter logic. These commands all begin with a semicolon.
Exit is :quit
To read a file from the "functions" directory and delivers it line by line to the interpreter :import filename
Creates a file in the functions directory containing the commands in the substack in stack position #0 :export filename
Execute a python command using exec and push the result onto the stack. Literal ?'s are replaced from left to right by popping values from the stack. :! command ?...
- ex 1) :! math.pi puts 3.14... onto the stack
- ex 2) :! math.pow(?, ?) will calculate #0 to the power of #1)
Enter puts the current line into the interpreter.
The up and down arrows move through the history.
^C will either clear the current entry or exit if there is nothing currently entered.
When the interface exits gracefully, the contents of the stack are written to the standard output.
Graphing
The interface now supports simple graphing. It has two modes, XY and X only. XY mode takes items from the stack in (X, Y) pairs and plots them. X mode uses the values on the stack as the y values and assigns an x value of 0 to the deepest item on the stack, and increments it for each item. They are then scaled to the display size and shown. You can switch to these modes by using the :graph X and :graph xy commands. The :graph command toggles between them. You can go back to the stack view with the :stack command.
You can enter new data and manipulate the stack at will while in the graph views, while they update in real time.
Here a sin wave is generated by decrementing a value (10.0) in 0.1 increments and running the math.sin instruction on it until it reaches zero.
Here the stack is cleared with the all autoloading function and then a countdown from 100 is created. The graph is a simple downward sloping line.
Kivy / Android
I ported a gui to Kivy which let me create an android app and get it onto the play store. Pretty cool.
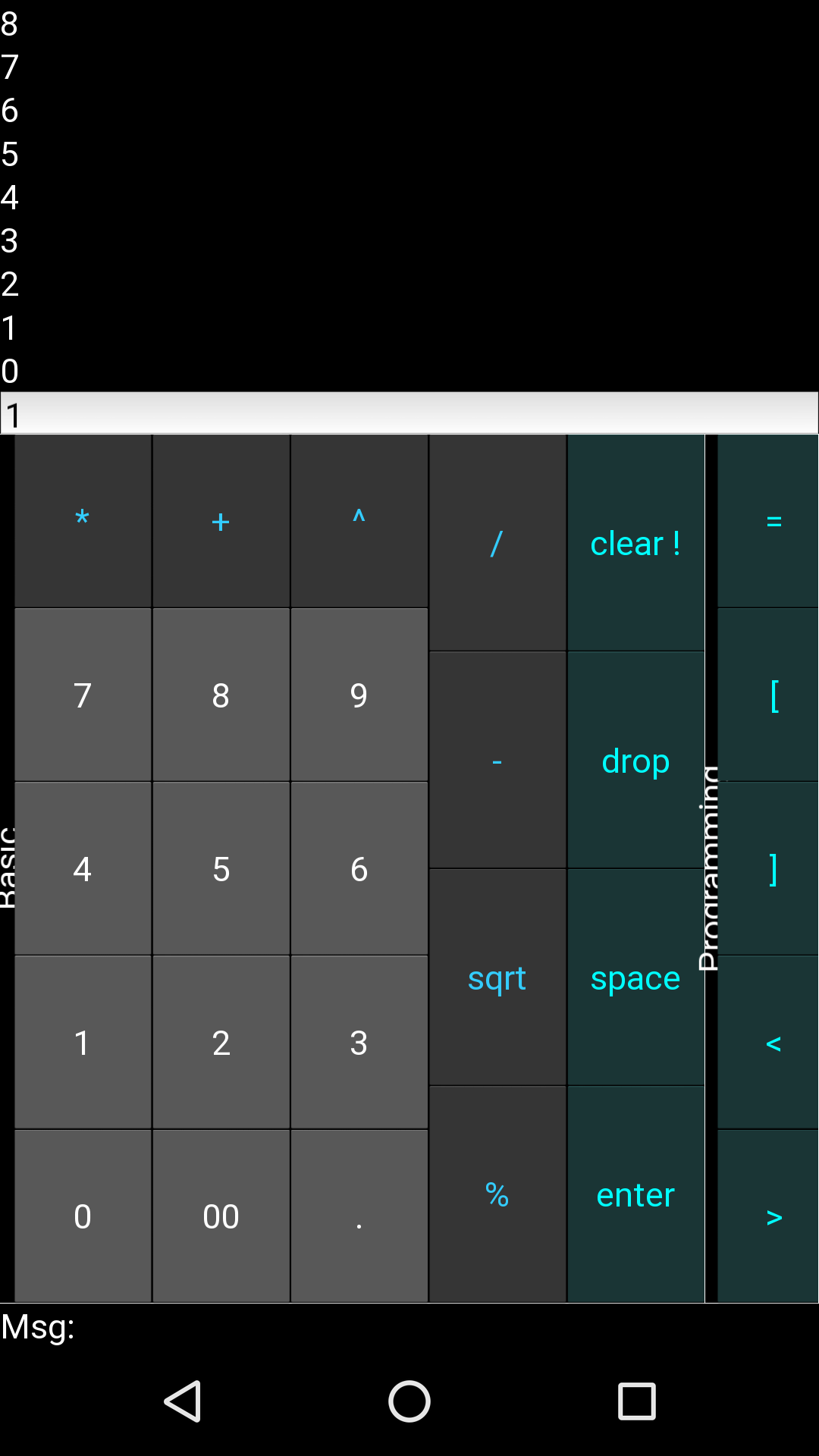
Download
Google Play store: https://play.google.com/store/apps/details?id=danomagnum.com.k2interface
Download the archive here. You can run python interface.py to get it going. The only dependencies should be python (2.7) and curses.
SVN access is here or svn co http://svn.danomagnum.com/svn/rpncalc/
 DanoMagnum.com
DanoMagnum.com